最速 降 线
最速降线问题
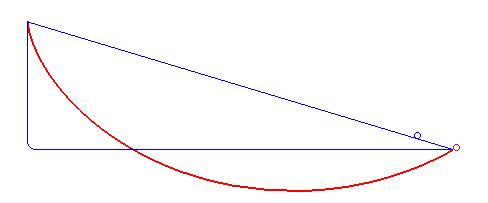
如何通俗易懂地解释最速降线?
最速降線問題
歷史
· 最下面那条线虽然平均速率大,但是路程相对来说又更大了。 而时间等于路程除以平均速率,折中之后最好的那条线就是速降线了,具体的就还是看@白书旭 的变分法, 发布于 2017-02-07, 赞同 3 5 条评论, 分享, 收藏 喜欢 收起 , 继续浏览内容, 知乎, 发现更大的世界, 打开, 浏览器, 继续, 写回答, 2 个回答
变分法与最速降线的证明
什么是最速降线?它又有何奇妙的性质呢?
最速降线的数学模型—变分法
· 变分法 最速降线 证明 极值 固有值 边界条件 函数 曲线 方程 函式
最速降曲线问题_sanlyshi’s front-end road-CSDN博客_最速下降曲线
· 最速降线Brachistochrone Problem证明参考数学之美: 两点之间最快的路径推导只需下落垂直高度,就可以知道这点的速度根据能量守恒定律,12mv2=mgy\frac{1}{2}mv^2 = mgy 得 v=2gy‾‾‾‾√v = \sqrt{2gy},对于路径s上的每一点,ds=dx2+dy2‾‾‾‾‾‾‾‾‾‾√=1+y′2‾‾‾‾‾‾‾√dxds = \sqrt{dx^2
· 就被称之为最速降线问题,是由意大利科学家伽利略在1630年提出的。 当时伽利略认为这个曲线是一个圆,可是这显然是一个错误的答案,17世纪的数学家约翰,伯努利、牛顿、莱布尼兹和伯努利家族的成员都找到了这条曲线,这条曲线又被称作 最速降线
由能量守恒,几种情况到达底部的速度是一样的,而曲线越陡,一开始获得的速度就越大,跑的就越快,再综合考虑路程问题,就是最降速曲线了。, 如图,如果上图为速度时间曲线的话,蓝线和红线最后的速度一样,但蓝方却多走了三角形ABC, 面积的路程。, 成名要乘早,大概就是这个意思吧, 发布于 2019-06-09, 继续浏览内容,
让我们先来看一个动图,, 最速降线。, 图片来源,维基百科。, 我们发现三个小球中在红色曲线上运动的小球最先到达最右侧的终点。, 这似乎有些违背直觉,因为上图中的红色曲线是最长的啊,小球在上面的运动时间应该更长才是啊?, 但事实真相并没有这么简单,下面我们就来系统的研究一下这条红色的曲线—— 最速降线 …
最速曲线_百度百科
简介
有了这些预备知识,我们来看看最速降线问题。 我们知道能量守恒,而动能和势能相互转化,下落的过程,就是势能转化成动能的过程。 所以,
变分法与最速降线问题_zhusf的博客-CSDN博客
· 最速降线在建筑中也有着美妙的应用。我国古建筑中的“大屋顶”,从侧面看上去,“等腰三角形”的两腰不是线段,而是两段最速降线。按照这样的原理设计,在夏日暴雨时,可以使落在屋顶上的雨水,以最快的速度流走,从而对房屋起到保护的作用。
下降时间 t t t 是曲线 y = y x y=yx y = y x 的泛函,最速降线就是 t y ty t y 的极值。因此最速降线必然满足泛函极值的必要条件。 因此最速降线必然满足泛函极值的必要条件。
最速 降 线
最速降线
最速降线问题, 问题, 在只考虑重力的作用的情况下,一质点从点A沿某条曲线到点B,问怎样的曲线能使所需时间最短?, 这一问题被称为最速降线问题(Brachistochrone),由约翰·伯努利在1696年提出来挑战欧洲的数学家。, 1、费马原理与斯涅耳定理, 约翰·伯努利的证明实际上非常巧妙,利用了费马原理,一束光从A点传播到B点总是沿着尽可能快的路径。, 从费马原理实际上可
《自然极值》系列——5,最速降线的故事
关于最速降线问题?
最速降线问题_百度百科
简介
Leave a Comment